This post is going to be about an integral identity called the product rule. This identity is going to be central to an efficient scheme for computing the energy-laplacian matrix for the serpinski gasket. It’s also cool.

In regular normal one-dimensional calculus, we define the derivative:

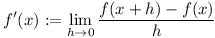
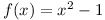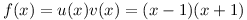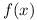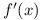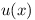Let’s explore some of the properties. Some functions can be split into a product of two other functions. For example, can be split into two functions in the following way: . If is of this form, then knowing a rule for determining from and 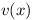might be valuable and save a good deal of effort. If you want to, you might want to stop reading and try to figure out a way to do this yourself. It will be rewarding even if you give up and keep reading.

Our first step in trying to figure out this rule is simply to use the definition of a derivative.

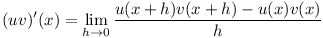
What would be a nice form for this to take? If the right side would perhaps contain either

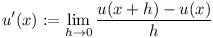
or

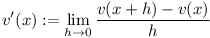
then the formula would be very nice: it would simply express the derivative of 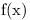in terms of the derivatives of its parts.

With that motivation in mind, I’m going to try to refactor the expression for the derivative of 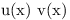. We assume that the functions involved are contintuous.

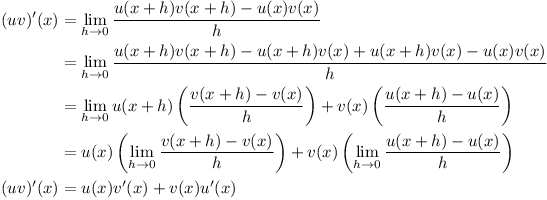
I learned this under the name of the product rule.

We can use this fact about derivatives to learn a fact about integrals. We use newton’s Fundamental Theorem of Calculus:

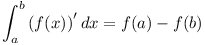
On the function :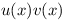

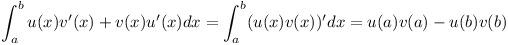
for any two functions.